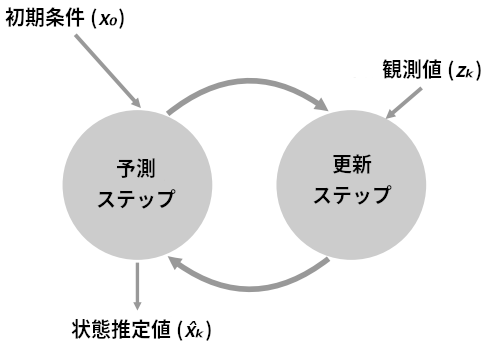
第 2 章 離散ベイズフィルタ
カルマンフィルタはベイズフィルタと呼ばれるフィルタの区分に属する。たいていの教科書でカルマンフィルタを扱うときは、まずベイズ統計の公式を示し、それをカルマンフィルタの式に変形することで紹介することが多い。しかし、その議論は非常に抽象的であることがほとんどだ。
そういったアプローチでは数学のいくつかの分野に関する非常に深い理解が必要とされ、問題設定や解法を直感的なレベルで理解する仕事の多くは読者に任されている。
これから私はこの話題を異なる方法で解説する。これは Dieter Fox と Sebastian Thrun による著作 Probabilistic Robotics1を大いに参考にしている。彼らは廊下を移動するロボットを使った例でベイズ統計を直感的に説明している──私は犬を使う。犬は好きだし、動きがロボットより予測できないので興味深いフィルタリングの問題が現れる。私が調べた限り、この例が出版された論文に登場したのは Dieter Fox らによる 1999 年の論文2が最初で、その後 2003 年の論文3でさらに完全な例が示されている。Sebastian Thrun は Udacity の Artificial Intelligence for Robotics という素晴らしいコースを担当しており、そこでも同じ定式化が使われている。もし動画を視聴する方が好みなら、本書を離れてこのコースの最初の数講義を視聴しておくのを強く勧める。それから本書に戻ってくれば、ベイズ統計をさらに深く理解できるだろう。
g-h フィルタと同じように、簡単な思考実験を通してフィルタリングと追跡で確率を使えないかどうかを見ていく。
2.1 犬の追跡
簡単な問題から始める。私たちの職場はドッグフレンドリーで、仕事に犬を連れて来る人がいるとする。犬はたまにオフィスを離れて廊下を進んでいくことがあるので、このときに犬を追跡したい。ある日のハッカソンで誰かが犬の首輪に付けるソナーセンサーを開発した。このソナーセンサーは信号を発信して反響を受信し、反響が返ってくる時間から開いたドアの前にいるかどうかを判定する。また犬の歩行を関知し、どちら側に歩いたかを報告することもできる。このセンサーは Wi-Fi を通じてネットワークにつながっており、一秒ごとに新しいデータを送信する。
私は自分の飼っている犬サイモンを追跡しようと思って、サイモンの首輪にセンサーを付けて Python を立ち上げ、建物の中を動き回るサイモンを追跡するコードを書く準備を整えた。一見すると、これは不可能に思えるかもしれない。サイモンの首輪にあるセンサーの送られて来るのは「ドア」「右に移動」「廊下」「右に移動」「廊下」といった情報だけなのだ。この情報からどうすればサイモンの居場所が分かるというのか?
問題の状況をプロットしやすくするために、廊下には 10 個の位置しか存在しないとする。10 個の位置は \(0\) から \(9\) までの整数で表され、\(1\) が \(0\) の右隣である。また後で明らかになる理由により、廊下は環状 (または長方形状) と仮定する。例えば位置 \(9\) から右に移動すると位置 \(0\) となる。
センサーからの信号を受け取り始めるとき、サイモンが廊下の特定の位置にいると信じる理由は何もないとする。つまり私の頭の中では、サイモンが任意の位置にいる確率は全て等しい。位置は 10 個あるから、任意の位置にサイモンがいる確率は \(1/10\) である。
サイモンの位置に関する信念を NumPy 配列を使って表現しよう。Python のリストも使えるかもしれないが、NumPy 配列だけが持つ機能が後で必要になる:
import numpy as np
belief = np.array([1/10]*10)
print(belief)[0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1]ベイズ統計学では、これを事前分布 (prior) と呼ぶ。観測値やその他の情報を取り入れる前に抱く確率が事前分布である。より正確な言葉を使えば、上のコードにおける belief は事前確率分布 (prior probability distribution) と呼ばれる。確率分布 (probability distribution) とは起こり得る全ての事象の確率を集めたものを言う。定義により、確率分布の和は 1 である必要がある: 何かしらの事象は必ず起きるからだ。確率分布は起こり得る全ての事象とそれぞれの確率を一覧にして示す。
あなたは間違いなく確率を使ったことがある──「今日の降水確率は 30% です」などと聞いたことがあるはずだ。一つ前の段落もそのような確率の使い方をしている。しかしベイズ統計学が確率論において革命的だったのは、確率を単一の事象に対する信念として扱った点である。例を示そう。もし私が公平なコインを無限回投げたら、50% では表が、50% では裏が出る。この考え方はベイズ統計学と区別して頻度主義的統計学 (frequentist statistics) と呼ばれる。頻度主義的統計学では、確率の議論は事象が発生する頻度に基づいて行われる。
私がコインを投げて、どこかに落ちたとする。コインはどちらを向いていると私は信じるだろうか? 頻度主義的統計学はこれに関して何も言わない: コインを何度も投げれば 50% が表になると言うだけだ。ある意味で、現在のコインの状態に関する確率を考えるのは意味がない: 現在のコインは表か裏のどちらかであり、ただ私たちにはそれが分からないというだけだ。一方ベイズ統計学では確率を一つの事象に関する信念として扱う──つまり、私が投げたそのコインが表を向いているはずだという私の信念 (を支える知識) の強さが 50% だと解釈される。信念 という言葉に違和感を覚える人もいるかもしれない。日常会話で使われる「信念」には「証拠はないがとにかく信じる」という含みがある。しかし本書 (およびベイズ統計学) で「信念」という言葉は、私たちが持つ知識の強さの指標を表すときにだけ使われる。さらに読み進めれば理解できるだろう。
ベイズ統計学は過去の情報 (事前分布) を考えに入れる。雨が降るのが 100 日ごとに 4 日だと観測結果から分かったなら、次の日に雨が降る確率は \(1/25\) だと言うことができる。ただ気象予報は普通このように行われない。今日雨が降っていて前線が停滞しているなら、明日も雨が降る確率が高い。こういった気象予報にもベイズ確率は使われている。
実際の問題に取り組むとき、統計学者は頻度主義的手法とベイズ的手法の両方を使い分ける。事前分布を見つけるのが困難あるいは不可能で、頻度主義的手法が力を発揮する場合もある。ただ本書では事前分布は必ず見つかるものとする。私が何かの確率について話をするとき、それは与えられた過去の事象を考えに入れたとき特定の物事が真になる確率 (知識の強さ) を意味している。つまり私が確率の話をするときはベイズ的なアプローチを取る。
話を戻して、次は廊下の地図を作ろう。最初の二つのドアは隣り合っていて、もう一つのドアは遠くにあるとする。ドアは \(1\) で、壁は \(0\) で表す:
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])サイモンから送られて来るデータをネットワークから受信し始めると、センサーから最初に送られてきたデータは「ドア」だった。センサーは必ず正しい答えを返すとしばらく仮定しよう。このときサイモンはドアの前にいることが分かるが、どのドアだろうか? 三つあるドアの中で特定のドアの前にいる可能性が高いと信じる理由はない。このような場合には、それぞれのドアに等しい確率を割り当てることになる。全てのドアの確率が同じで、ドアは三つあるから、各ドアに \(1/3\) の確率を割り当てればよい:
import kf_book.book_plots as book_plots
from kf_book.book_plots import figsize, set_figsize
import matplotlib.pyplot as plt
belief = np.array([1/3, 1/3, 0, 0, 0, 0, 0, 0, 1/3, 0])
book_plots.bar_plot(belief)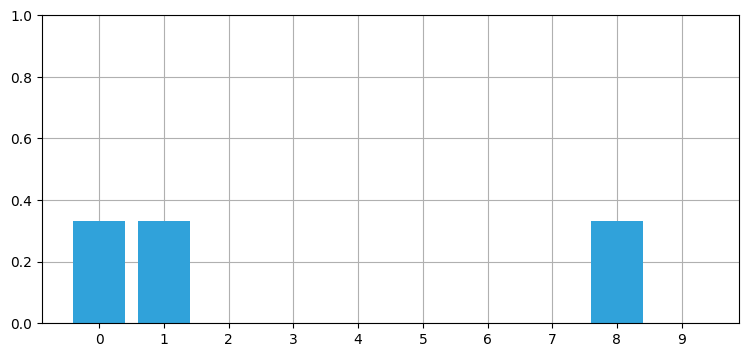
この分布は \(n\) 個の結果を観測する確率を記述する離散分布であり、カテゴリカル分布 (categorical distribution) と呼ばれる。またサイモンの位置に関して複数の信念が存在するので、多峰性分布 (multimordal distribution) でもある。もちろんサイモンが異なる位置に同時に存在していると主張しているのではない: それぞれの位置にサイモンがいるという知識の強さが同じだと言っているだけだ。観測値を取り入れることで、私の (ベイズ的な意味での) 信念は「位置 \(0\) にいる確率が 33.3%、位置 \(1\) にいる確率が 33.3%、位置 \(8\) にいる確率が 33.3%」に変化した。
二つの点で分布は改善された。廊下の位置が不可能であるとして棄却され、他の位置に関する信念の強さは 10% から 33% に増加した。この現象は知識を取り入れるたびに必ず起こる: 知識が増えるにつれ、確率は 100% に近づく。
モード (mode, 最頻値・峰とも) という用語について少し解説する。数値の集合、例えば \(\{1, 2, 2, 2, 3, 3, 4\}\) が与えられたとき、出現回数が最も多い数値をモードと呼ぶ。この集合では \(2\) がモードである。モードが複数ある分布もある。例えば集合 \(\{1, 2, 2, 2, 3, 3, 4, 4, 4\}\) では \(2\) と \(4\) がどちらも三回出現するので、\(2\) と \(4\) がモードとなる。モードを一つだけ持つ前者のような集合を単峰 (unimodal) であると言い、モードが複数ある後者のような集合を多峰 (multimodal) であると言う。
この分布に関連してもう一つ、ヒストグラム (histogram) という用語も紹介しておく。数値の集合からなる分布を図として表したものをヒストグラムと呼ぶ。上で示した棒グラフはヒストグラムである。
上のコードでは belief 配列を手で書いているが、同じ配列をコードで計算するにはどうすればよいだろうか? ドアは 1 で、壁は 0 で表しているから、hallway 配列に確率を乗じればよい。次のようになる:
belief = hallway * (1/3)
print(belief)[0.333 0.333 0. 0. 0. 0. 0. 0. 0.333 0. ]2.2 センサーの出力から情報を取り出す
一旦 Python は脇に置いて、今考えている問題についてさらに考えよう。サイモンに付いているセンサーから次の情報が出力されたとする:
- ドア
- 右に移動
- ドア
サイモンの位置は分かるだろうか? もちろん分かる! ドアと壁の配置を考えれば、この観測値が得られる初期位置は左端 (位置 \(0\)) しかない。よって現在サイモンは位置 \(2\) にいると自信を持って答えられる。もし納得できないなら、サイモンが二つ目のドアまたは三つ目のドアの前にいる状態から始まった場合を考えてみるとよい。するとサイモンが右に動いたとき、センサーは必ず「壁」を返す。これは実際の出力と異なるから、仮定した開始位置は間違っている。同様の議論は他の全ての開始位置に対して行えるから、現在サイモンは二番目のドアの前にいるというのが唯一の可能性となる。このとき私たちの信念はこうなる:
belief = np.array([0., 1., 0., 0., 0., 0., 0., 0., 0., 0.])私は正確な答えが早く得られるようドアと壁の配置とセンサーの出力を調整した。現実の問題はこれほど簡単ではない。しかし直感はつかめたはずだ──センサーからの一つ目の出力はサイモンの位置に関して低い確率 (\(0.33\)) しか与えないが、位置が更新されセンサーからの新しい出力が手に入ると、位置はより正確に分かるようになる。読者はこんなふうに (正しく) 考えるかもしれない: 廊下が非常に長くてドアが大量にあったとしても、位置の更新とセンサーの出力がいくつかあればサイモンの位置が分かる (あるいは可能性のある位置が少数に絞られる) のではないか、と。センサーの出力がマッチする開始位置が少ないときにこれは可能になる。
この解決法をコードにすることもできるが、まずは悪影響を及ぼす可能性のある現実世界の要因を考えよう。
2.3 センサーの出力に含まれるノイズ
完璧なセンサーはまず存在しない。サイモンがドアの前にいても、毛づくろいをしていたり廊下と平行に立っていなかったりすればセンサーが誤った出力を生成する可能性がある。そのためセンサーから「ドア」という出力を受け取ったとしても、サイモンがドアの前にいる確率を \(1/3\) とはできない。各ドアには \(1/3\) より小さい確率を割り当て、それ以外の位置にも小さい確率を割り当てる必要がある。例えばこんな風に:
[.31, .31, .01, .01, .01, .01, .01, .01, .31, .01]
一見すると問題は解けないように思えるかもしれない。センサーにノイズがあると、全てのデータを疑う必要が生じる。どんなときも確かなことが分からないとしたら、そこから結論を得るなど可能なのか?
この問題は確率を使うと答えられる。サイモンの位置について確率的な信念を考えるのは先ほどの例で慣れたと思う。次はセンサーのノイズによる不確実性に対処しなければならない。
「ドア」という出力が得られたとする。加えて、センサーが正しい答えを出力する確率が間違った答えを出力する確率の三倍だとしよう。このときドアの位置にいるという確率を他の位置にいる確率の三倍にしなければならない。愚直にこれを行うと確率分布を表さない配列となってしまうが、それを直す方法をすぐに示す。
この処理を Python コードとしてみてみよう。ここで z が観測値を表す。観測値は z または y で表すのがフィルタリングの文献における慣習となっている。プログラマーとして私は意味のある変数名を選びたい気持ちはあるのだが、読者には他の文献や他の人が書いたフィルタリングコードも読めるようになってほしいと思っている。そのため本書では省略した名前を使う:
def update_belief(hall, belief, z, correct_scale):
for i, val in enumerate(hall):
if val == z:
belief[i] *= correct_scale
belief = np.array([0.1] * 10)
reading = 1 # 1 = 「ドア」
update_belief(hallway, belief, z=reading, correct_scale=3.)
print('信念:', belief)
print('和 =', sum(belief))
plt.figure()
book_plots.bar_plot(belief)信念: [0.3 0.3 0.1 0.1 0.1 0.1 0.1 0.1 0.3 0.1]
和 = 1.6000000000000003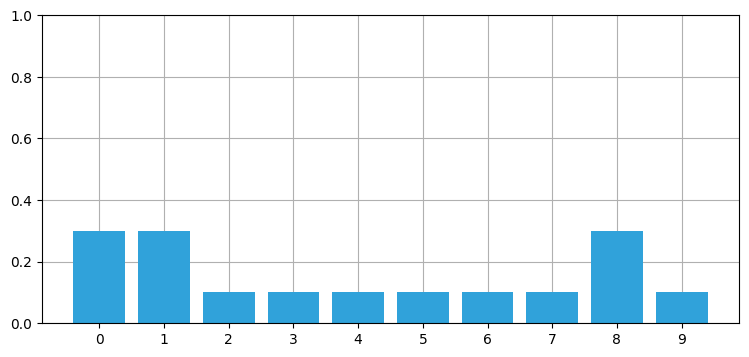
計算された belief は和が \(1\) でないので、確率分布ではない。しかしその点を除けば、コードは正しい処理を行っている──ドアに割り当てられた確率 (\(0.3\)) は壁に割り当てられた確率 (\(0.1\)) の三倍である。後は belief を正規化して、確率の和が \(1\) となるようにするだけだ。正規化は各要素を和で割ることで行える。NumPy なら簡単にできる:
belief / sum(belief)array([0.188, 0.188, 0.062, 0.062, 0.062, 0.062, 0.062, 0.062, 0.188,
0.062])FilterPy では normalize 関数として実装されている:
from filterpy.discrete_bayes import normalize
normalize(belief)
「正しい確率が間違う確率の三倍」というのは少しおかしな仮定に思えるから、センサーが正しい値を出力する確率 \(prob_{correct}\) が分かっていて、そこからスケーリング係数 \(scale\) (上のコードにおける correct_scale) を計算するようにしよう。この計算は次の式で行える。ここで \(prob_{incorrect}\) はセンサーの出力が誤っている確率であり、\(prob_{correct} + prob_{incorrect} = 1\) が成り立つ:
それから、for ループは望ましくない。一般に NumPy では for を避けるべきとされる。NumPy は C や Fortran で実装されており、for ループを避けることができれば実行速度が 100 倍になることも珍しくない。
どうすれば for ループを取り除けるだろうか? NumPy では真偽値の配列を使って配列にアクセスでき、真偽値の配列は真偽演算子で作成できる。例えば廊下にあるドアは次のように見つけられる:
hallway == 1array([ True, True, False, False, False, False, False, False, True,
False])配列の添え字に真偽値配列を使うと、真偽値配列で True の場所が返る。よって上述の for は次のコードで置き換えられる:
belief[hall==z] *= scale
このとき z に等しい要素だけに scale が乗じられる。
NumPy の使い方の解説は本書の範囲を超える。以降では最初から NumPy らしいコードを書いて、新しい手法が使われるときに説明を加えることにする。NumPy を使うのが初めてなら、NumPy らしい高速なコードを書く方法についてのブログ記事や動画が数多く存在するので参考にしてほしい。
改善されたバージョンを示す:
from filterpy.discrete_bayes import normalize
def scaled_update(hall, belief, z, z_prob):
scale = z_prob / (1. - z_prob)
belief[hall==z] *= scale
normalize(belief)
belief = np.array([0.1] * 10)
scaled_update(hallway, belief, z=1, z_prob=.75)
print('和 =', sum(belief))
print('ドアの確率 =', belief[0])
print('壁の確率 =', belief[2])
book_plots.bar_plot(belief, ylim=(0, .3))和 = 1.0
ドアの確率 = 0.1875
壁の確率 = 0.06249999999999999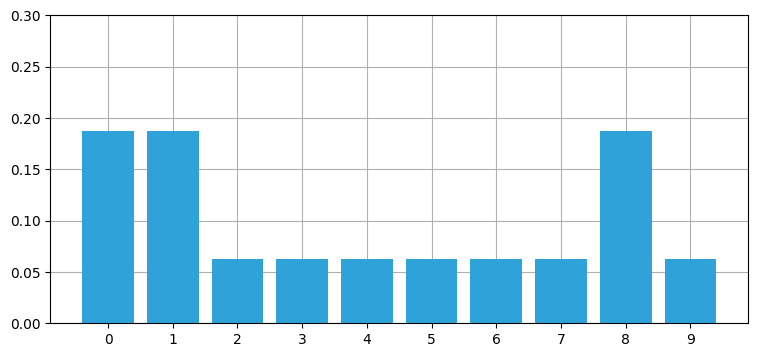
belief の和が \(1\) になったこと、そしてドアの確率が壁の確率の三倍であることが出力から分かる。またドアの確率が \(1/3\) より小さく、壁の確率が \(0\) より大きくなるはずだという直感的な予想は結果と一致する。最後に、それぞれのドアとそれぞれの壁を区別できるだけの情報が与えられていないために、全てのドアと全ての壁の同じ確率はそれぞれ同じになるはずだという直感的な予想も結果と一致する。
この結果は事後分布 (posterior) と呼ばれる。省略せずに言えば事後確率分布 (posterior probability distribution) である。事後確率分布は観測値の情報を組み込んだ後の確率分布を意味する (この文脈で posterior は after と同じ意味になる)。復習しておくと、事前確率分布は観測された情報を含める前の確率分布だった。
もう一つ尤度 (likelihood) という用語もここで登場する。belief[hall==z] *= scale の計算では、与えられた観測値から各位置にサイモンがいたと考えられる (相対的な) 度合いを計算している。これがまさに尤度である。尤度の和は 1 にならないので、尤度は確率分布ではない。
事前分布、事後分布、尤度の間には次の関係がある:
フィルタの出力について話をするとき、予測を行う前の状態を事前状態または予測状態と呼び、観測値を用いた更新を行った後の状態を事後状態または推定状態と呼ぶ。
こういった用語はほぼ全ての文献で広く使われるので、よく理解しておくことが重要である。
先ほどの scaled_update 関数はこの計算を行うのだろうか? 実は行っている。コードの形を変えると分かりやすくなる:
def scaled_update(hall, belief, z, z_prob):
scale = z_prob / (1. - z_prob)
likelihood = np.ones(len(hall))
likelihood[hall==z] *= scale
return normalize(likelihood * belief)この関数は完全に一般的とは言えない。観測値と廊下をマッチさせる方法や廊下に関する知識がハードコードされている。関数は必ず一般的な形で書けないかどうかを考えるべきである。ここでは尤度の計算を関数から取り出して、呼び出し側に計算させるようにできる。
事後分布を計算するアルゴリズムの完全な実装を示す:
def update(likelihood, prior):
return normalize(likelihood * prior)
尤度 likelihood の計算は問題によって異なる。例えばセンサーが返すのは整数 1 または 0 ではなく、ドアの前にいる確率を示す \(0\) から \(1\) の float かもしれない。またはセンサーが返すのはコンピュータービジョンを使ったぼんやりした形状で、ドアとマッチするかどうかを自分で確率的に計算する必要があるかもしれない。あるいはソナーを使って測定した距離を返す可能性もある。尤度の計算方法はそれぞれの場合で異なる。本書では様々な例を使って異なる尤度計算の方法を学ぶ。
FilterPy は update 関数を実装している。考えてきた例に対する完全に一般的な形の解法を示す:
from filterpy.discrete_bayes import update
def lh_hallway(hall, z, z_prob):
""" 計測値が廊下の各位置にマッチする尤度を計算する。 """
try:
scale = z_prob / (1. - z_prob)
except ZeroDivisionError:
scale = 1e8
likelihood = np.ones(len(hall))
likelihood[hall==z] *= scale
return likelihood
belief = np.array([0.1] * 10)
likelihood = lh_hallway(hallway, z=1, z_prob=.75)
update(likelihood, belief)array([0.188, 0.188, 0.062, 0.062, 0.062, 0.062, 0.062, 0.062, 0.188,
0.062])2.4 移動の組み込み
観測値をいくつか取得すると厳密な解がすぐに手に入っていたことを思い出してほしい。あれは完璧なセンサーが存在する仮想的な世界での話だった。センサーにノイズがある場合でも厳密な解を見つけられるだろうか?
残念ながら、答えは否である。センサーの出力が非常に複雑な廊下の地図と完璧に合っていたとしても、サイモンが特定の位置にいると 100% の自信を持って言い切ることはできない──どこまでいっても、センサーからの出力が全て間違っている可能性が (ごく小さいものの) 存在する! 典型的な状況ではセンサーはたいてい正しい値を出力するので、私たちは解に 100% に近い自信を持てる。ただ 100% になることは決してない。状況が複雑になってきたが、まずは数式をプログラムしてみよう。
まず簡単な場合を考える──移動センサーは完璧だと仮定する。そのセンサーがサイモンは右に位置一つ分だけ移動したと報告したとする。このとき信念を表す belief 配列はどう変化するだろうか?
移動前の belief を一つずつ右にずらせばよい、というのは少し考えれば理解できることを願う。移動前にサイモンが 50% の確率で位置 \(3\) にいると考えていたなら、右に位置一つ分だけ移動した後にサイモンが位置 \(4\) にいると信じる度合いは 50% であるはずである。廊下は環状だったから、シフトはモジュロ算術を使って行える:
def perfect_predict(belief, move):
"""
move が非負なら、位置を move 個だけ右に動かす。
move が負なら、位置を -move 個だけ左に動かす。
"""
n = len(belief)
result = np.zeros(n)
for i in range(n):
result[i] = belief[(i-move) % n]
return result
belief = np.array([.35, .1, .2, .3, 0, 0, 0, 0, 0, .05])
plt.subplot(121)
book_plots.bar_plot(belief, title='Before prediction', ylim=(0, .4))
belief = perfect_predict(belief, 1)
plt.subplot(122)
book_plots.bar_plot(belief, title='After prediction', ylim=(0, .4))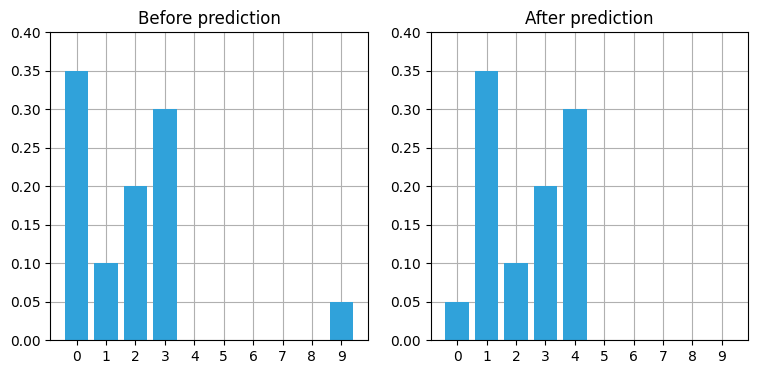
全ての位置に対する信念が一つずつ右に移動し、配列の端は最初に戻っていることが分かる。
次のセルでは移動をアニメーションで確認できるようになっている。スライダーを使うと時間を前後に動かせる。ここではサイモンが廊下を動き回るのをシミュレートしているだけであり、新しい観測値は組み込んでいない。そのため確率分布は形を変えず、位置だけが変化する:
from ipywidgets import interact, IntSlider
belief = np.array([.35, .1, .2, .3, 0, 0, 0, 0, 0, .05])
perfect_beliefs = []
for _ in range(20):
# サイモンが位置一つ分だけ右に移動する
belief = perfect_predict(belief, 1)
perfect_beliefs.append(belief)
def simulate(time_step):
book_plots.bar_plot(perfect_beliefs[time_step], ylim=(0, .4))
plt.show()
interact(simulate, time_step=IntSlider(value=0, max=len(perfect_beliefs)-1));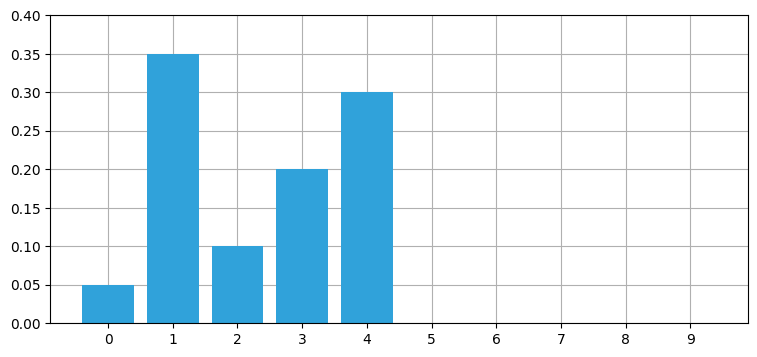
2.5 用語の整理
少し足を止めて、用語を確認する。前章でも説明はしたが、理解を確かなものにするために少し時間を割こう。
系 (system) は私たちがモデル化やフィルタリングを行おうとしているものを言う。今の例ではサイモンという犬が系となる。状態 (state) は現在の系を表す構成または値を言う。今の例ではサイモンの位置が状態となる。しかし実際の状態が分かることはまずない。この事実は「フィルタは系の推定状態 (estimated state) を生成する」と表現される。実際に話を進めるときは推定状態のことを状態と呼ぶこともあるので、注意して文脈を理解する必要がある。
系の振る舞いに関する知識を使った予測と観測値を使った更新の一サイクルを、状態または系の発展 (evolution) と呼ぶ。これは時間発展 (time evolution) を省略した言葉である。発展を系伝播 (system propagation) と呼ぶこともある。これらはどれも系の状態が時間の経過とともに変わっていく様子を表す。フィルタでは離散的なステップ (例えば一秒) だけ離れた時刻を考えることが多い。私たちの犬追跡システムでは犬の位置が状態であり、時間発展は一定時間が経過したときに犬の位置が変わることを言う。
系の振る舞いはプロセスモデル (process model) でモデル化される。私たちのプロセスモデルは「犬は各タイムステップで位置を変える」というものである。これは犬の振る舞いの正確なモデルとは言えない。モデルに含まれる誤差は系誤差 (system error) あるいはプロセス誤差 (process error) と呼ばれる。
プロセスモデルを使った予測で得られるのは新しい事前分布である。時間が進み、観測値を活用する前に行った予測の結果を事前分布は表す。
一つ例を考えよう。現在の犬が \(17~\text{m}\) の位置にいて、エポックは二秒の長さであり、犬は \(15~\text{m/s}\) で進んでいるとする。二秒後の犬の位置はどう予測できるだろうか?
もちろん
となる。変数の上にある横棒は、観測値などの情報を取り入れずに計算された値 (予測値) であることを示す。プロセスモデルを表す方程式は一般的に次のように書ける:
\(x_k\) は現在の位置 (状態) を表す。犬が \(17~\text{m}\) 地点にいるなら \(x_k = 17\) となる。
\(f_x(\bullet)\) は \(x\) に対する状態伝播であり、一度のタイムステップにおける \(x_k\) の変化量を表す (\(\bullet\) は引数の名前や個数が定まっていないことを表す)。私たちの例では状態伝播で \(15 \times 2\) のような計算が行われるから、 \(f_x(\bullet)\) は次のように定義できる:
2.6 予測に不確実性を加える
perfect_predict() は観測値が完璧なことを仮定していたが、センサーには必ずノイズが含まれる。サイモンが位置一つ分だけ移動したとセンサーが報告したときに、本当は二つ移動していたり、全く移動していなかったりしたらどうすればよいだろうか? 手の施しようのない問題に思えるかもしれないが、モデルを作って何が起こるかを見よう。
センサーから報告される移動量の観測値が正しい確率が 80%、実際の値より一つ大きい確率が 10%、実際の値より一つ小さい確率が 10% と仮定する。例えば移動量の観測値が \(4\) (右に四つ移動したことを表す) なら、サイモンは 80% の確率で右に四つ移動し、10% の確率で右に三つ、10% の確率で右に五つ移動している。
新しい信念を表す配列 belief の各要素は三つの異なる状況に対する確率を取り入れなければならない。例えば報告された移動量が \(2\) だとする。もし最初サイモンが位置 \(3\) にいることを 100% 確信しているなら、現在の信念は位置 \(5\) に 80% 、位置 \(4\) に 10%、 位置 \(6\) に 10% となる。これをコードにしてみよう:
def predict_move(belief, move, p_under, p_correct, p_over):
n = len(belief)
prior = np.zeros(n)
for i in range(n):
prior[i] = (
belief[(i-move) % n] * p_correct +
belief[(i-move-1) % n] * p_over +
belief[(i-move+1) % n] * p_under)
return prior
belief = [0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]
prior = predict_move(belief, 2, .1, .8, .1)
book_plots.plot_belief_vs_prior(belief, prior)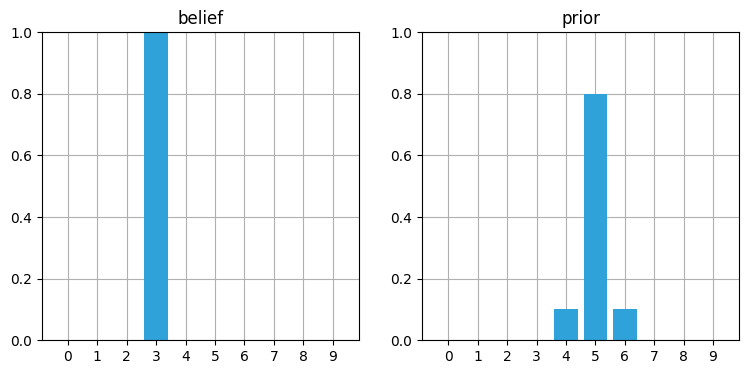
正しく動いているように思える。信念が 100% でない場合はどうだろうか?
belief = [0, 0, .4, .6, 0, 0, 0, 0, 0, 0]
prior = predict_move(belief, 2, .1, .8, .1)
book_plots.plot_belief_vs_prior(belief, prior)
priorarray([0. , 0. , 0. , 0.04, 0.38, 0.52, 0.06, 0. , 0. , 0. ])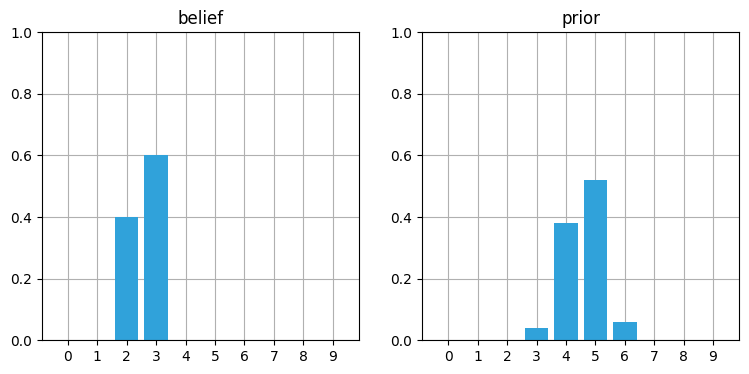
結果は複雑だが、同じ計算は頭の中でもできるだろう。例えば位置 \(3\) の信念 \(0.04\) は \(0.4\) の信念 (位置 \(2\)) で観測値から一つ小さい値を採用したときの値として計算される。また位置 \(4\) の信念 \(0.38\) は次のように計算される: \(0.4\) の信念 (位置 \(2\)) から観測値通りに二つ移動するときの確率 (\(0.8 \times 0.4\)) と、\(0.6\) の信念 (位置 \(3\)) から観測値より小さく一つ移動するときの確率 (\(0.6 \times 0.1\)) を足すと \(0.38\) になる。観測値より大きく移動する確率がここで考えに入らないのは、位置 \(2\) または位置 \(3\) から三つ移動すると位置 \(4\) を飛び越してしまうためだ。以降の説明は大部分がこのステップの理解を前提としているので、深く理解できるまでいくつか例を試してみることを強く勧める。
更新後の確率分布を見て不思議に思うかもしれない。上の例では二つの位置に \(0.4\) と \(0.6\) がある確率分布から始まっているのに対して、更新後の確率分布では山が低く、さらに裾も大きくなっている。
この現象は偶然ではないし、この現象を起こすために数値を選んだわけでもない──予測で必ず起きる。センサーにノイズが含まれると、予測のたびに情報の一部が失われる。では予測を無限回行った状況を想像してほしい──どうなるだろうか? ステップごとに情報を失うなら、いずれ情報が全て失われ、そのとき belief 配列には同じ数値だけとなるはずだ。100 回の反復で試してみよう。次のグラフは対話的になっており、スライダーでステップ数を変えられる:
belief = np.array([1.0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
predict_beliefs = []
for i in range(100):
belief = predict_move(belief, 1, .1, .8, .1)
predict_beliefs.append(belief)
print('最後の信念:', belief)
# プロットを対話的にする。
def show_prior(step):
book_plots.bar_plot(predict_beliefs[step-1])
plt.title(f'Step {step}')
plt.show()
interact(show_prior, step=IntSlider(value=1, max=len(predict_beliefs)));最後の信念: [0.104 0.103 0.101 0.099 0.097 0.096 0.097 0.099 0.101 0.103]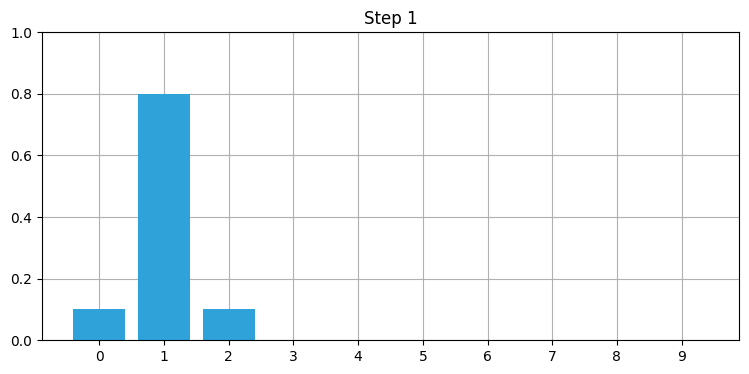
print('最終的な信念:', belief)最終的な信念: [0.104 0.103 0.101 0.099 0.097 0.096 0.097 0.099 0.101 0.103]位置 \(0\) に 100% の確信を持って開始したにもかかわらず、100 反復後には情報がほぼ全て失われる。数字を変更して、更新回数を変えたときにどうなるかを確認してみてほしい。例えば 100 反復だと情報はほんの少し残るが、50 反復だとだいぶ残っており、200 反復だと事実上全ての情報が失われる。
オンラインで HTML として本書を読んでいる人に向けて、出力のアニメーションを示しておく:
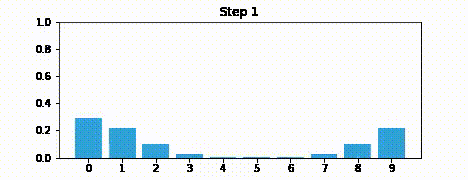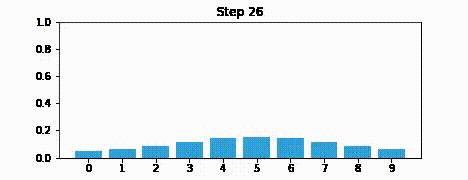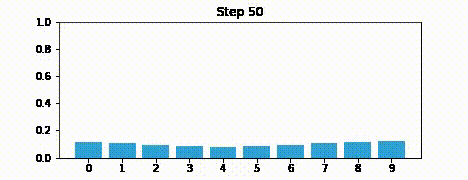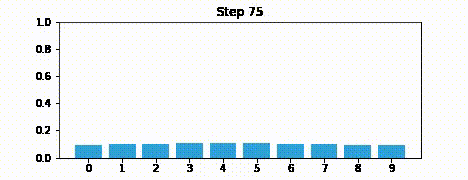
これからはアニメーションを gif 画像として載せることはしない。ぜひ自分の PC に IPython をインストールして Jupyter Notebook として本書を読んでほしい。そうすればセルを全て実行して、アニメーションを表示させることができる。ただ受動的に読むだけではなくコードを使って実験するのは非常に重要である。
2.7 畳み込みを使った一般化
ここまでは移動量の誤差は最大でも \(1\) であるという仮定を置いたが、誤差が \(2\) や \(3\)、あるいはもっと大きくなる可能性もある。プログラマーとして私たちは、いつものごとく全てのケースに対応できるようコードの一般化を行いたい。
これは畳み込み (convolution) を使うと簡単に解決できる。畳み込みは特定の関数を使って関数を改変する手法であり、今の例ではセンサーの誤差関数を使って確率分布を改変するのに利用できる。実は上で実装した predict_move() では知らないうちに畳み込みを使っていた。畳み込みの形式的な定義を次に示す:
ここで \(f \ast g\) は \(g\) による畳み込みを \(f\) に適用することを表す記号であり、乗算の記号ではない。
積分は連続関数に対してしか使えないが、今使っているのは離散関数だった。積分を総和に、関数呼び出しの括弧を配列アクセスの鍵括弧に置き換えれば離散関数用の畳み込みとなる:
predict_move 関数がこの等式を計算していることは実装と見比べると分かる ──この関数が計算しているのは同様の形の積の和である。
畳み込みの優れた解説動画が Khan Academy にあり、Wikipedia には分かりやすいアニメーションが載っている。ただ一般的なアイデアは今の私たちでも簡単に理解できる。カーネルと呼ばれる配列を別の配列の上でスライドさせ、カーネルの各要素と二つ目の配列の対応する要素の積の和を現在のセルの値とする、というものだ。上述の例では移動量が正しい確率が \(0.8\)、一つ大きい確率が \(0.1\)、一つ小さい確率が \(0.1\) だったので、カーネルは [0.1, 0.8, 0.1] という配列になる。後は畳み込み対象の配列の各要素をループし、配列の対応する部分とカーネルの積を計算し、その和を結果とするだけだ。信念が確率分布であることを強調するために、以下では名前を pdf としている:
def predict_move_convolution(pdf, offset, kernel):
N = len(pdf)
kN = len(kernel)
width = int((kN - 1) / 2)
prior = np.zeros(N)
for i in range(N):
for k in range(kN):
index = (i + (k-width) - offset) % N
prior[i] += pdf[index] * kernel[k]
return priorアルゴリズムはこの通りなのだが、この実装は非常に遅い。SciPy のndimage.filters モジュールは畳み込みを行う convolve 関数を提供している。この関数を predict_move_convolution と同じインターフェースで使うには畳み込みの前に pdf を offset だけずらす必要があるが、これは numpyp.roll 関数を使うと行える。この二つの関数があれば、移動の予測を行う畳み込みの処理を一行で実装できる:
convolve(np.roll(pdf, offset), kernel, mode='wrap')
FilterPy は discrete_bayes.predict 関数でこれを実装する:
from filterpy.discrete_bayes import predict
belief = [.05, .05, .05, .05, .55, .05, .05, .05, .05, .05]
prior = predict(belief, offset=1, kernel=[.1, .8, .1])
book_plots.plot_belief_vs_prior(belief, prior, ylim=(0,0.6))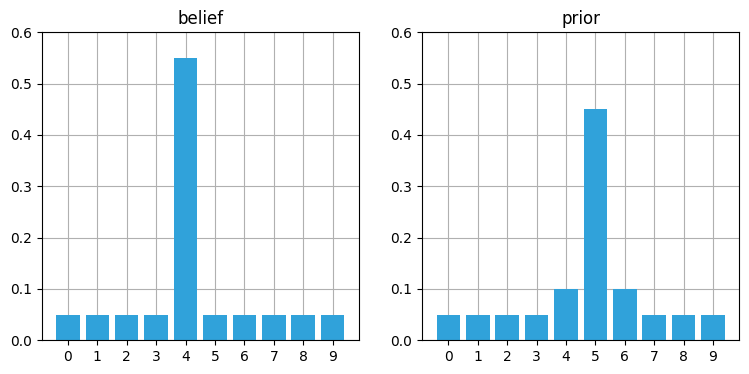
中央の三つの要素だけが変化している。位置 \(4\) と位置 \(6\) の値は
と計算され、位置 \(5\) の値は次のように計算される:
\(1\) より大きな移動量と非対称なカーネルを用いたときでも位置が正しくシフトされることを確認しよう:
prior = predict(belief, offset=3, kernel=[.05, .05, .6, .2, .1])
book_plots.plot_belief_vs_prior(belief, prior, ylim=(0,0.6))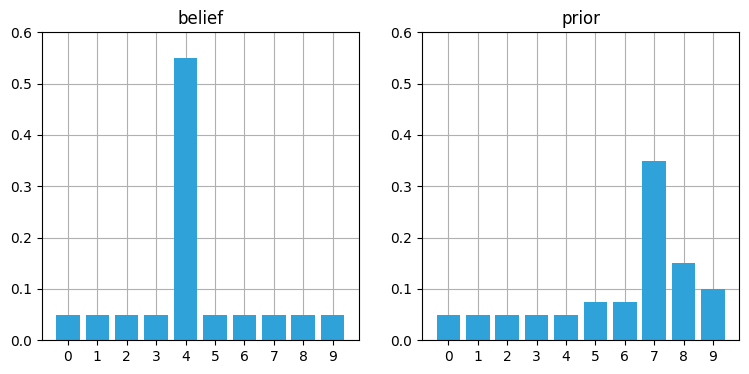
位置は正しく三つシフトされ、位置 \(7\) より近くに比べて位置 \(7\) より遠くに大きな確率が割り当てられているので、正しく動いているように見える。
ここで行っていることの理解を確認してほしい。私たちは犬の移動場所を予測していて、確率の畳み込みを使って事前分布を計算している。
確率を使っていないなら、次の等式を使っていただろう:
このとき犬がいる場所の予測値は現在位置に移動量を足したものに等しい。\(10~\text{m}\) 地点にいる犬が \(5~\text{m}\) 動いたなら、現在 \(15~\text{m}\) 地点にいる。これほど簡単なこともない。しかし私たちは確率でこの系をモデル化しているから、数式は次の形になる:
ここでは現在位置の確率的な推定値と移動量の確率的な推定値の畳み込みを行っている。考え方は同じだが、数式としては少し違う。\(\mathbf{x}\) が太字なのは、この記号が数値の配列を表すためだ。
2.8 観測値の組み込み
予測によって情報が失われるので、系はすぐに知識を持たない状態になってしまうと思うかもしれない。しかし予測の後には観測値を取り入れて推定値を計算する更新ステップが存在し、この更新により私たちの知識は更新される。更新ステップの出力は次の予測ステップに渡される。次の予測で正確さが失われるが、またその後にある更新で正確さが向上する。
直感的に考えてみよう。簡単なケースとして、じっとして動かない犬を追跡する問題を考える。このとき予測では犬が動かないという予測を立てる。犬が実際に動かなければ、フィルタは正確な位置の推定値に素早く収束する。その後、誰かがキッチンで電子レンジを使って、犬がキッチンに向かって飛び出していったとする。あなたはそれを知らないので次の予測でも犬が同じ位置にいるという予測を立てるが、観測値は違うことを示す。このとき観測値を取り入れていくに従って、信念は廊下をキッチンに向かって広がっていく。エポック (予測-観測サイクル) のたびに、彼がじっとしている信念は小さくなり、キッチンに向かって驚くべき速さですっ飛んでいった信念が大きくなる。
以上が直感的に分かることだ。数式からは何が分かるだろうか?
更新ステップと予測ステップは既にプログラムにしたから、後はこの二つを組み合わせれば、ついに犬の追跡機の実装が完了する!!! どうなるか見てみよう。サイモンは位置 \(0\) からスタートして、エポックごとに位置一つ分ずつ右に移動すると仮定したときの観測値を入力とする。現実世界のアプリケーションと同様に、彼の位置に関する知識は全く存在せず、全ての位置に対して等しい確率を割りあてた状態でフィルタリングを開始する。
from filterpy.discrete_bayes import update
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])
prior = np.array([.1] * 10)
likelihood = lh_hallway(hallway, z=1, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))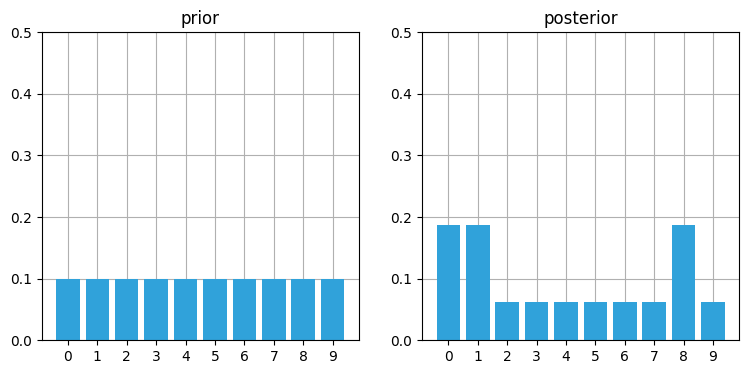
初回の更新ではそれぞれドアの位置に高い確率が、壁の位置に低い確率が割り振られる。
kernel = (.1, .8, .1)
prior = predict(posterior, 1, kernel)
book_plots.plot_prior_vs_posterior(prior, posterior, True, ylim=(0,.5))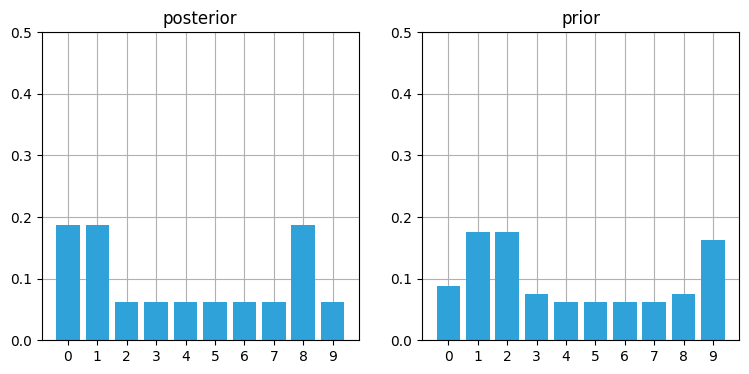
予測ステップにより確率は右にひとつシフトされ、加えて山が少しだけ平坦になる4。次の観測更新で何が起こるかに注目してほしい:
likelihood = lh_hallway(hallway, z=1, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))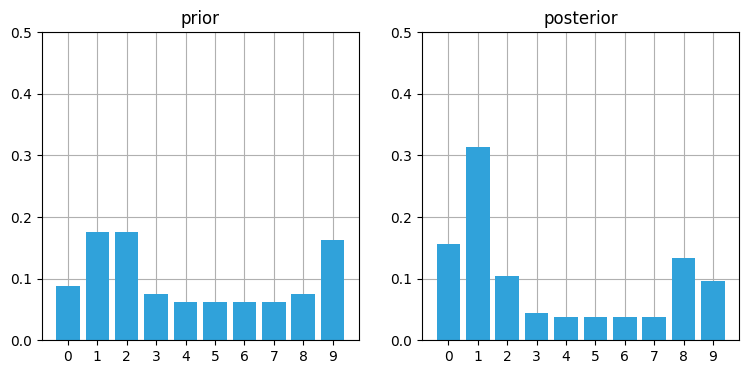
位置 \(1\) の確率が高くなったのが分かる。これは位置 \(0\) から始まって、ドアを観測し、右に一つ移動し、またドアを観測するという (正しい) ケースに対応する。他のどの位置に最初いたとしても、これらの観測値が得られる可能性が位置 \(1\) より高くなることはない。次の更新では壁が観測される:
prior = predict(posterior, 1, kernel)
likelihood = lh_hallway(hallway, z=0, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))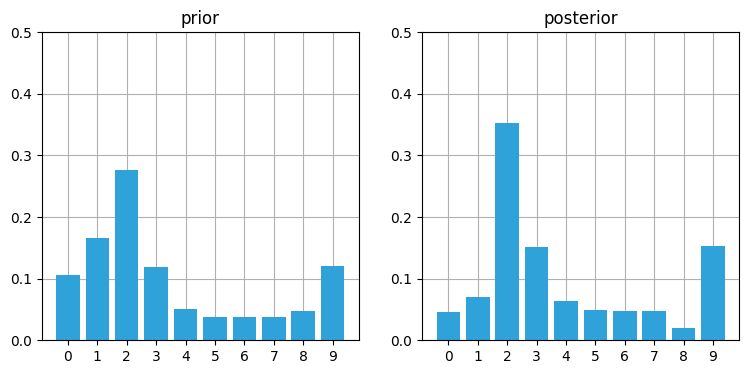
面白くなってきた! 位置 \(2\) に 35% という非常に高いバーが現れている。これは他のバーと比べて二倍以上の高さであり、一つ前のグラフにおける位置 \(1\) の確率 (約 31%) より 4% 高い。もう一サイクル進めると、正しい位置の確率がさらに高くなる:
prior = predict(posterior, 1, kernel)
likelihood = lh_hallway(hallway, z=0, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))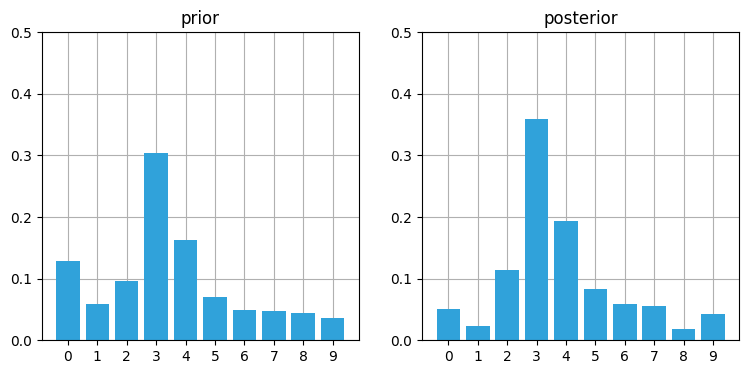
私は重要な問題を一つ無視している: 予測ステップ用のモーションセンサーがあるという仮定が存在する。電子レンジについて話をしたとき、サイモンが突然走り出すことは想定していないものの、(モーションセンサーがなくても) サイモンが走っているという信念はいずれ大きくなると話した。しかしこの処理を行うコードは書いていない。プロセスモデルの変化を測定していないときに、それを検出・推定するにはどうすればよいだろうか?
ここではこの問題を扱わないことにする。以降の章ではこの推定のための数学を学ぶが、今の段階ではこれまでに示したアルゴリズムを学ぶだけでも大きな仕事だ。プロセスモデルの変化への適応という問題は非常に重要であるものの、必要な数学はまだ手にしていない。そのため本章ではこれ以降、移動量を測定できるセンサーがサイモンに付いていると仮定してこの問題を無視する。
この形は g-h フィルタと同じだが、誤差をパーセンテージで表すことで \(g\) と \(h\) を暗黙に使っている。離散ベイズアルゴリズムを g-h フィルタの一種として表すこともできるが、そうするとこのフィルタのロジックが分かりにくくなってしまうだろう。
離散ベイズフィルタの公式を示す:
\(\mathcal L\) は尤度関数を表すのに普通使われる記号だから、ここでも使った。\(\ast\) は畳み込み、\(\cdot\) は要素同士の積、\(\|\bullet\|\) は正規化を表す。尤度と事前分布の積は正規化しないと \(\mathbf{x}\) が確率分布 (和が \(1\)) にならない。
これは疑似コードとしても表せる:
初期化
- 状態に関する信念を初期化する。
予測
- 系の振る舞いを利用して、次のタイムステップにおける状態を予測する。
- 予測の不確実性に応じて信念を調整する。
更新
- 観測値と正確さに関する信念を取得する。
- 観測値が各状態にマッチする度合い (尤度) を計算する。
- その尤度で状態に関する信念を更新する。
カルマンフィルタでもこれと全く同じアルゴリズムが使われる。変わるのは計算の細部だけである。
この形のアルゴリズムを予測子修正子法 (predictor-corrector method) と呼ぶことがある。予測をして、それを修正するためだ。
これをアニメーションにしてみよう。まずフィルタリングを行って各ステップの結果をプロットする関数を書く。ドアの位置は黒、事前分布はオレンジ、事後分布は青で示した。黒い縦線はサイモンの実際の位置を表す。ただしサイモンの位置はフィルタの出力ではない──シミュレートしているから分かるだけだ。
def discrete_bayes_sim(prior, kernel, measurements, z_prob, hallway):
posterior = np.array([.1]*10)
priors, posteriors = [], []
for i, z in enumerate(measurements):
prior = predict(posterior, 1, kernel)
priors.append(prior)
likelihood = lh_hallway(hallway, z, z_prob)
posterior = update(likelihood, prior)
posteriors.append(posterior)
return priors, posteriors
def plot_posterior(hallway, posteriors, i):
plt.title('Posterior')
book_plots.bar_plot(hallway, c='k')
book_plots.bar_plot(posteriors[i], ylim=(0, 1.0))
plt.axvline(i % len(hallway), lw=5)
plt.show()
def plot_prior(hallway, priors, i):
plt.title('Prior')
book_plots.bar_plot(hallway, c='k')
book_plots.bar_plot(priors[i], ylim=(0, 1.0), c='#ff8015')
plt.axvline(i % len(hallway), lw=5)
plt.show()
def animate_discrete_bayes(hallway, priors, posteriors):
def animate(step):
step -= 1
i = step // 2
if step % 2 == 0:
plot_prior(hallway, priors, i)
else:
plot_posterior(hallway, posteriors, i)
return animateフィルタを実行してアニメーションにする (キーボードの矢印キーを使うと一ステップずつスライダーを移動できる):
# 以下の値を変えるとシミュレーションの結果が変わる。
kernel = (.1, .8, .1)
z_prob = 1.0
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])
# 観測値にノイズはないとする。
zs = [hallway[i % len(hallway)] for i in range(50)]
priors, posteriors = discrete_bayes_sim(prior, kernel, zs, z_prob, hallway)
interact(animate_discrete_bayes(hallway, priors, posteriors),
step=IntSlider(value=1, min=1, max=len(zs)*2));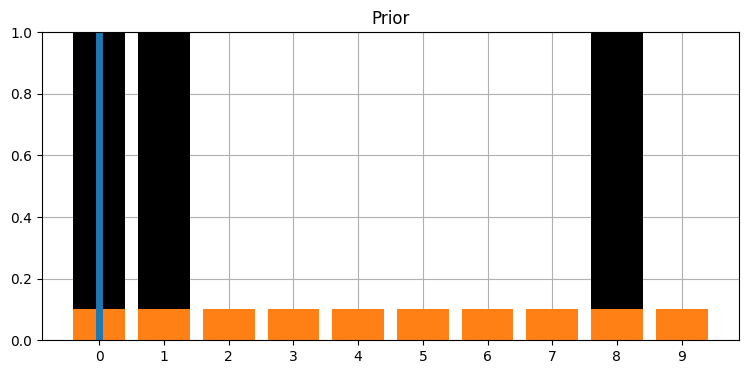
これでフィルタリングの進む様子を確認できる。事前分布では位置が移動して正確さが減少し、事後分布では位置が移動せず (観測値を取り入れるために) 正確さが増しているのが分かるだろう。ここでは z_prob = 1.0 として観測を完璧にしている: 完璧でない観測の影響は次節で見る。
もう一つ注目すべき点として、推定値はサイモンがドアの前にいるとき高くなり、壁の前にいるとき低くなる。これは直感的にも納得できるはずだ。ドアの個数は壁の個数よりも少ないから、センサーがドアの前にいると報告したときは位置がより正確に定まる。そのため長い間ドアを観測できないと、私たちはサイモンの居場所に自信を持てなくなる。
2.10 不正確なセンサーデータの影響
関数への入力が常に正しいセンサーデータなのはおかしいと言って、上の結果を疑う人がいるかもしれない。このコードはフィルタなのだから、入力されたデータにノイズがあっても取り除けるはずだ。本当だろうか?
実験をプログラム・可視化しやすくするために、ドアと壁がほぼ互い違いに並ぶよう廊下の形状を変更する。まずは六個の正しい観測値を与えてアルゴリズムを実行しよう:
hallway = np.array([1, 0, 1, 0, 0]*2)
kernel = (.1, .8, .1)
prior = np.array([.1] * 10)
zs = [1, 0, 1, 0, 0, 1]
z_prob = 0.75
priors, posteriors = discrete_bayes_sim(prior, kernel, zs, z_prob, hallway)
interact(animate_discrete_bayes(hallway, priors, posteriors),
step=IntSlider(value=12, min=1, max=len(zs)*2));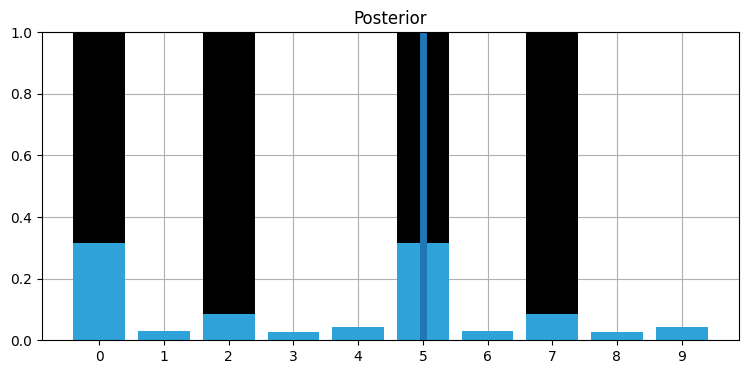
位置 \(0\) または 位置 \(5\) から開始した確率が高いことが特定されている。フィルタに与えた [1,0,1,0,0] というドアと壁のパターンに一致するのがこの二つの位置であるためだ。続いてノイズの入った観測値を入力してみよう。次の観測値は \(0\) であるべきだが、\(1\) とする:
measurements = [1, 0, 1, 0, 0, 1, 1]
priors, posteriors = discrete_bayes_sim(prior, kernel, measurements, z_prob, hallway);
plot_posterior(hallway, posteriors, 6)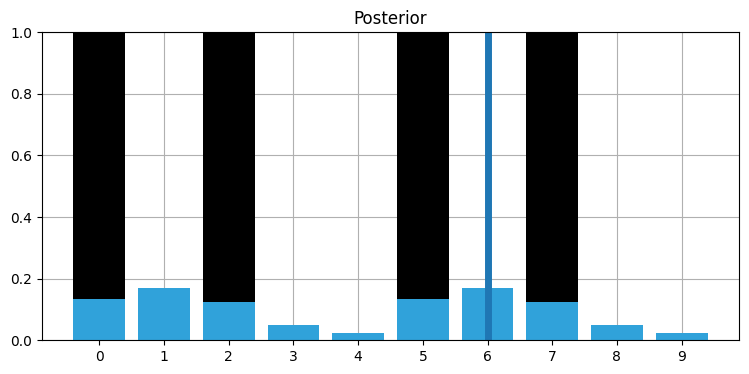
正しくない観測値が一つ入力されただけで、私たちの知識 (信念) は大きく変化した。これ以降は正しい観測値が入力されるとしてみよう:
with figsize(y=5.5):
measurements = [1, 0, 1, 0, 0, 1, 1, 1, 0, 0]
for i, m in enumerate(measurements):
likelihood = lh_hallway(hallway, z=m, z_prob=.75)
posterior = update(likelihood, prior)
prior = predict(posterior, 1, kernel)
plt.subplot(5, 2, i+1)
book_plots.bar_plot(posterior, ylim=(0, .4), title=f'step {i+1}')
plt.tight_layout()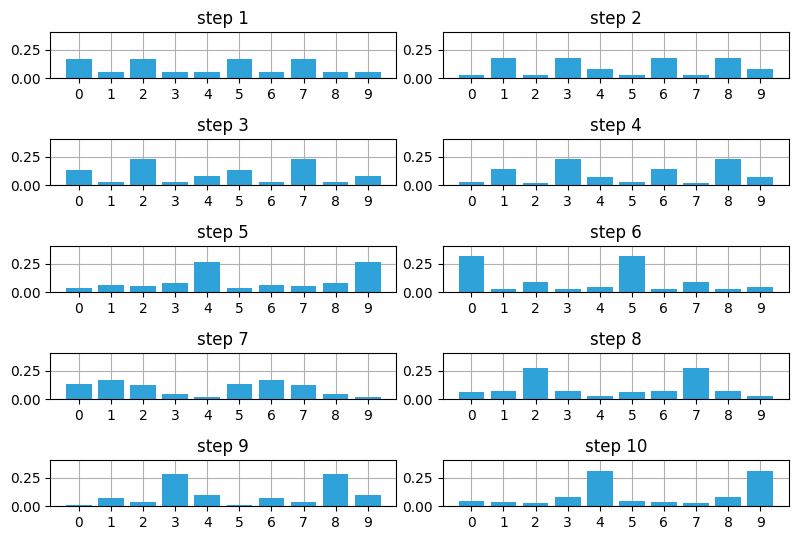
正しい入力が続くと観測値に加わったノイズによる影響は取り除かれ、確率分布はサイモンの位置として可能性の最も高い (二つの) 位置に収束している。
2.11 欠点と制限
私が選んだ例の単純さに騙されてはいけない。離散ベイズフィルタはロバストで完全なフィルタであり、このコードで現実世界の問題を解くこともできる。もし多峰性の離散フィルタが必要なら、離散ベイズフィルタで問題はない。
ただそうは言っても、このフィルタにはいくつか制限があるので使われることは少ない。離散ベイズフィルタが持つ制限を取り払うのが本書の以降の章におけるモチベーションとなる。
離散ベイズフィルタの一つ目の問題はスケーラビリティである。サイモンを追跡する問題では位置を表す変数が一つあるだけだったが、通常私たちが考える問題では大きな空間を移動する複数の物体を追跡する必要がある。現実的には、最低でもサイモンの \((x,y)\) 座標を追跡できるのが望ましいだろうし、おそらく \((\dot{x},\dot{y})\) の追跡も必要だろう。多次元の場合は解説していないが、一次元配列の代わりに多次元配列を使って各 (離散) 位置における確率を考えれば行える。update と predict は配列に含まれる全ての値を更新しなければならないので、四つの変数が存在する単純な問題でも \(O(n^4)\) の実行時間がタイムステップごとに必要になる。現実的なフィルタだと十個以上の変数を持つ場合もあるので、途方もない計算資源が要求される。
二つ目の問題は離散ベイズフィルタが離散的なことである。私たちの住む世界は連続的だ。信念をヒストグラムで図示していることからも分かるように、離散ベイズフィルタを使うときは出力が離散的な点の集合になるよう問題をモデル化しなければならない。\(100~\text{m}\) の廊下を精度 \(1~\text{cm}\) でモデル化するには 10,000 個の位置が必要であり、更新と予測では 10,000 個の異なる確率に対する計算が行われることになる。この問題は次元を追加すれば指数的に悪化する: \(100{\times}100~\text{m²}\) の庭を \(1~\text{cm}\) 精度でモデル化するには 100,000,000 個の印を用意しなければならない。
三つ目の問題は離散ベイズフィルタが多峰性なことである。最後の例ではサイモンが位置 \(4\) または位置 \(9\) にいる確率が高い信念が手に入っている。なお、これが必ず問題になるわけではない: 例えば本書の後半で登場する粒子フィルタは多峰性であり、多峰性であるために使われる。しかし車に搭載される GPS が「A 通りにいる確率が 40% で、B 通りにいる確率が 30% です」などと報告するのを想像してみてほしい。
四つ目の問題は状態の変化を観測する必要があることである。サイモンの移動量を測定するモーションセンサーが必要になる。この問題を避ける方法は存在するが、この章で紹介すると話が複雑になるので紹介しなかった。これまで述べてきた問題が存在するので、この点について深堀りはしない。
このような問題はあるものの、離散ベイズフィルタが扱える小さい問題を考えているときであれば私は離散ベイズフィルタを使って問題を解くだろう。このフィルタは実装・デバッグ・理解が非常に簡単で、実装者にとって都合がいい。
2.12 追跡と制御
ここまでは自走する物体を受動的に追跡してきた。続いてよく似た次の問題を考える。私は倉庫の自動化を担当していて、顧客から注文があった商品を取ってくる作業をロボットに行わせたいとする。おそらく一番簡単なのはロボットが特定の線路上だけを通れるようにすることだ。ロボットに目的地を設定して送り出せば後はそこまで自動的に移動してくれればよいのだが、ロボットが通る線路やロボットに搭載されるモーターは完璧でない。車輪が滑ったりモーターの精度が悪かったりすると、ロボットは指定された場所に移動できない可能性が高くなる。ロボットはいくつもあるから、衝突を起こさないためにそれらの位置を知る必要がある。
そこでセンサーが追加された。おそらく線路上に数フィートの間隔で磁石を配置して、ホールセンサーで通過した磁石の数を数えるのかもしれない。例えば 10 個目の磁石を観測したなら、そのロボットは 10 個目の磁石の位置にいる。もちろん磁石をいくつか飛ばしたり、一つの磁石を何度も数えたりすることもあるかもしれないから、いくらかの誤差は受け入れなければならない。磁石の数え上げはドアの検知とほぼ同じだから、前節のコードを使えばロボットを追跡できる。
しかしそれで終わりではない。どんなときでも情報を捨ててはいけないと私たちはこれまでに学んだ。もし情報があるなら、推定値を向上させるために利用しなければならない。ここで捨てようとしている情報は何だろうか? 各時点でロボットの車輪に与えている制御命令を私たちは知っている。例えば移動命令 (「右に一単位動け」「左に一単位動け」「動くな」のいずれか) を一秒に一度の頻度で送信するとしよう。「左に一単位動け」の命令を出したとすれば、今から一秒後にロボットは現在位置から一単位だけ左に移動すると期待できる。これは加速度を考えていないので単純になってはいるが、私は完全なロボット制御理論を教えたいわけではない。車輪とモーターは完璧でないから、「左に一単位動け」と命令したとしてもロボットの移動距離は \(0.9\) 単位や \(1.2\) 単位になる可能性がある。
これでフィルタリング処理の全容がはっきりした。サイモンを追跡する問題ではサイモンがずっと同じ方向に移動するという奇妙な仮定を置いていた! ロボットの移動はもっと予測しやすい。奇妙な仮定を使って疑わしい予測を立てるのではなく、ロボットに送った命令からまともな予測が立てられる! 具体的に言うと、predict 関数に渡す移動の尤度を表すカーネルをロボットに送った命令から計算できる。
2.13 ロボットの振る舞いのシミュレート
まず不完全なロボットをシミュレートする必要がある。このロボットには私たちから移動命令を送るのだが、移動距離が少しずれる可能性があり、搭載してあるセンサーが間違った値を返す可能性もある。
class Robot(object):
def __init__(self, track_len, kernel=[1.], sensor_accuracy=.9):
self.track_len = track_len
self.pos = 0
self.kernel = kernel
self.sensor_accuracy = sensor_accuracy
def move(self, distance=1):
""" 指定された方向に移動する。
確率的に移動距離へ誤差を加える。 """
self.pos += distance
# カーネルに従うような誤差を加える
r = random.random()
s = 0
offset = -(len(self.kernel) - 1) / 2
for k in self.kernel:
s += k
if r <= s:
break
offset += 1
self.pos = int((self.pos + offset) % self.track_len)
return self.pos
def sense(self):
pos = self.pos
# センサーの誤差を加える
if random.random() > self.sensor_accuracy:
if random.random() > 0.5:
pos += 1
else:
pos -= 1
return posこれでフィルタを書く準備が整った。仮定を変えて実行できるよう関数として書くことにする。ロボットは常に線路の最初の地点からスタートし、線路は 10 単位の長さを持つと仮定する: この 10 単位が何度も (例えば 10,000 単位の間) 繰り返されると思ってほしい。10 単位にしたのはプロットと考察を簡単にするためだ。
def robot_filter(iterations, kernel, sensor_accuracy,
move_distance, do_print=True):
track = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
prior = np.array([.9] + [0.01]*9)
posterior = prior[:]
normalize(prior)
robot = Robot(len(track), kernel, sensor_accuracy)
for i in range(iterations):
# ロボットを動かす
robot.move(distance=move_distance)
# 予測を行う
prior = predict(posterior, move_distance, kernel)
# フィルタを更新する
m = robot.sense()
likelihood = lh_hallway(track, m, sensor_accuracy)
posterior = update(likelihood, prior)
index = np.argmax(posterior)
if do_print:
print(f'時刻 {i}: 位置 {robot.pos}, 観測された位置 {m}')
conf = posterior[index] * 100
print(f' 推定された位置 {index}, 信頼度 {conf:.4f}%')
book_plots.bar_plot(posterior)
if do_print:
print()
print('最後の位置 ', robot.pos)
index = np.argmax(posterior)
print('''推定された位置 {}, '''
'''信頼度 {:.4f}%:'''.format(
index, posterior[index]*100))コードを読んで、理解できることを確認してほしい。まずは移動距離とセンサーに誤差がないものとして実行してみよう。コードが正しければ、フィルタはロボットの位置を誤差無く特定できるはずだ。出力を理解するのは多少面倒だが、更新/予測サイクルの動作の理解に少しでも不安があるなら時間をかけて注意深く読んで理解を深めてほしい:
import random
random.seed(3)
np.set_printoptions(precision=2, suppress=True, linewidth=60)
robot_filter(4, kernel=[1.], sensor_accuracy=.999,
move_distance=4, do_print=True)時刻 0: 位置 4, 観測された位置 4
推定された位置 4, 信頼度 99.9900%
時刻 1: 位置 8, 観測された位置 8
推定された位置 8, 信頼度 100.0000%
時刻 2: 位置 2, 観測された位置 2
推定された位置 2, 信頼度 100.0000%
時刻 3: 位置 6, 観測された位置 6
推定された位置 6, 信頼度 100.0000%
最後の位置 6
推定された位置 6, 信頼度 100.0000%: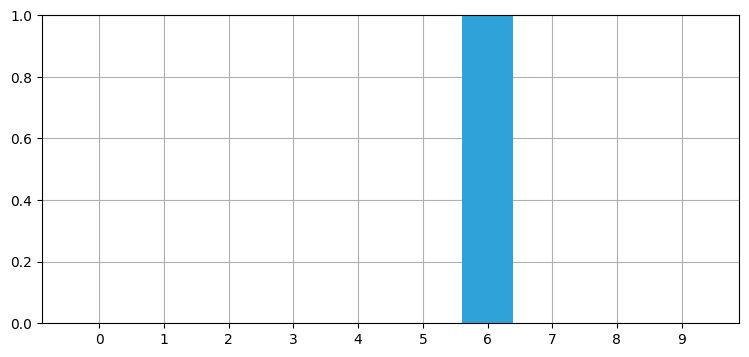
コードは完璧にロボットを追跡できているから、上のコードは正しく動作するようだとそれなりの自信が持てる。次はエラーを加えても大丈夫かどうかを確認しよう:
random.seed(2)
robot_filter(4, kernel=[.1, .8, .1], sensor_accuracy=.9,
move_distance=4, do_print=True)時刻 0: 位置 5, 観測された位置 4
推定された位置 4, 信頼度 96.0390%
時刻 1: 位置 8, 観測された位置 8
推定された位置 8, 信頼度 96.8094%
時刻 2: 位置 2, 観測された位置 2
推定された位置 2, 信頼度 96.9180%
時刻 3: 位置 6, 観測された位置 6
推定された位置 6, 信頼度 96.9331%
時刻 4: 位置 0, 観測された位置 0
推定された位置 0, 信頼度 96.9352%
最後の位置 0
推定された位置 0, 信頼度 96.9352%: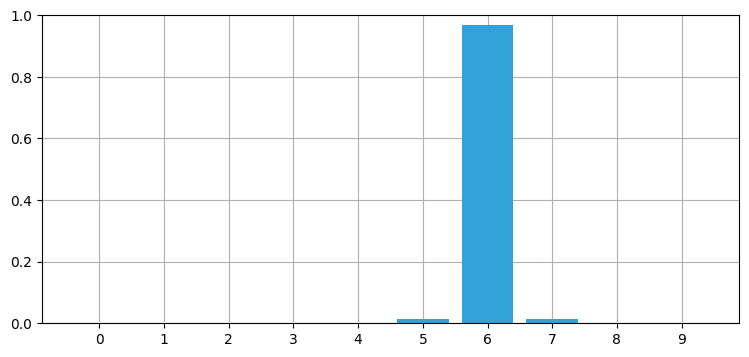
時刻 \(1\) で観測値に誤差があるものの、推定置には非常に高い信頼度がある。
続いて長いシミュレーションを実行して、フィルタが誤差にどう反応するかを見よう:
with figsize(y=5.5):
for i in range (4):
random.seed(3)
plt.subplot(221+i)
robot_filter(148+i, kernel=[.1, .8, .1],
sensor_accuracy=.8,
move_distance=4, do_print=False)
plt.title (f'Iteration {148 + i}')
plt.tight_layout()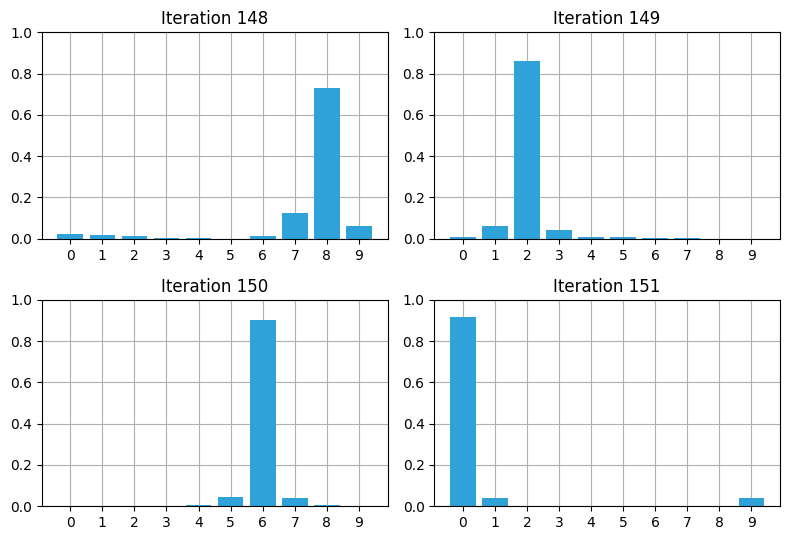
148 回目の反復で信頼度が下がっているものの、それからの数回でフィルタは推定値の信頼度が回復しているのが分かる。
2.14 ベイズの定理と全確率の定理
本章で使った数式は各時刻で手にしている情報について考えるだけで導出された。その中で私たちはベイズの定理 (Beyes' theorem) と全確率の定理 (total probability theorem) を発見している。
ベイズの定理を使うと、与えられた過去の情報からある事象の確率を計算する方法が分かる。
update 関数の実装では確率を次のように計算していた:
ベイズ確率を議論する数学的な用語はまだ紹介していないものの、この式はまさにベイズの定理である。本書に登場するフィルタは全てベイズの定理を言い換えたものと言える。次章ではベイズ確率に関する数学について学ぶが、これは次の等式で示される簡単なアイデアを様々な形で複雑に表現しているだけだ:
ここで \(\| \cdot \|\) は挟まれた式の正規化を表す。
この単純な洞察は廊下を歩き回る犬について考えることで得られた。しかし同じ等式はどんなフィルタリングの問題にも現れ、本書でも以降の全ての章で登場する。
同様に、予測ステップを実装する predict 関数では可能性のある複数の事象に対する確率の和を計算していた。この裏には統計学で全確率の定理として知られる定理がある。次章では必要になる数学を説明してから触れる。
今のところは、新しい情報を既存の情報に取り込むのがベイズの定理なのだと理解しておいてほしい。
2.15 まとめ
コードは非常に短いが、結果は素晴らしい! 本章ではベイズフィルタの一種を実装した。私たちが学んだのは、情報が何もない状態から始めて、ノイズの含まれるセンサーから情報を引き出す方法である。例で使ったセンサーには大きなノイズが含まれる (たいていのセンサーの精度は 80% より高い) ものの、サイモンのいる可能性を示す確率分布は素早く収束した。予測ステップでは必ず知識が失われるものの、新しい観測値を加えると (たとえ観測値にノイズが含まれていても) 知識が正確になり、このサイクルを繰り返せば確率分布が最も可能性の高い結果に収束することが分かった。
本書は主にカルマンフィルタについて話をする。カルマンフィルタで使われる数学は難しいが、その考え方は本章で使ったのと全く同じだ: ベイズ確率を使って観測値とプロセスモデルから推定値を計算する。
本章を理解できたなら、カルマンフィルタも理解・実装できる。これはどれだけ強調してもしすぎることはない。よく分かっていない部分があるなら、本章を読み直してコードをいじってみるべきだ。本書の残りの部分では本章で使ったアルゴリズムを拡張するので、離散ベイズフィルタの動作が分かっていないと理解できる望みはほとんどない。一方で、土台にある考え方──更新のときに観測値の尤度と事前分布を乗じて正規化すると、推定値がいずれ解に収束する──が理解できたのなら、後は数学を少し学べばカルマンフィルタを実装する準備が整う。
-
Sebastian Thrun, Wolfram Burgard, and Dieter Fox, Probabilistic Robotics, The MIT Press, 2005.[return]
-
Dieter Fox, Wolfram Burgard, and Sebastian Thrun, "Markov localization for mobile robots in dynamic environments." Journal of artificial intelligence research, 11, 1999, 391-427.[return]
-
Deter Fox, Jeffrey Hightower, Lin Liao, Dirk Schulz, and Gaetano Borriello, "Bayesian Filters for Location Estimation." IEEE Pervasive Computing, 2.3, 2003, 24-23.[return]
-
訳注: 上の図では、全ての位置に同じ確率を割り振る最初の信念を一度目の予測の結果とみなしている。[return]